Chọn lộ trình học
Tìm lộ trình phù hợp với bạn

Lộ trình Interactive SAT theo Lesson
Audio theo bài giảng
SAT Full Journey
Trọn Bộ Lộ Trình Chinh Phục SAT
Thành thạo dạng bài dữ liệu hai biến và biểu đồ phân tán trong SAT
Giới thiệu
Hiểu và phân tích dữ liệu hai biến và biểu đồ phân tán (scatterplots) là kỹ năng quan trọng trong phần toán SAT liên quan đến phân tích dữ liệu. Bài viết này hướng dẫn bạn từng bước làm chủ các khái niệm này.
Dữ liệu Hai Biến là gì?
Dữ liệu hai biến thể hiện mối quan hệ giữa hai loại biến khác nhau. Ví dụ:
– Số giờ học và điểm kiểm tra
– Lượng mưa và sản lượng cây trồng
Trong SAT, bạn thường cần phân tích dữ liệu hai biến để xác định xem thay đổi ở một biến sẽ ảnh hưởng thế nào đến biến còn lại.
Hiểu về Biểu đồ Phân tán (Scatterplot)
1. Biểu đồ Phân tán là gì?
Biểu đồ phân tán thể hiện các điểm dữ liệu riêng lẻ trên hệ trục tọa độ 2 chiều. Mỗi trục biểu diễn một biến. Các điểm này giúp ta quan sát xu hướng, mẫu hình và mối tương quan giữa hai biến.
Ví dụ: Trục hoành (x) biểu diễn giờ học, trục tung (y) biểu diễn điểm kiểm tra. Mỗi điểm trên biểu đồ đại diện cho 1 học sinh cụ thể.
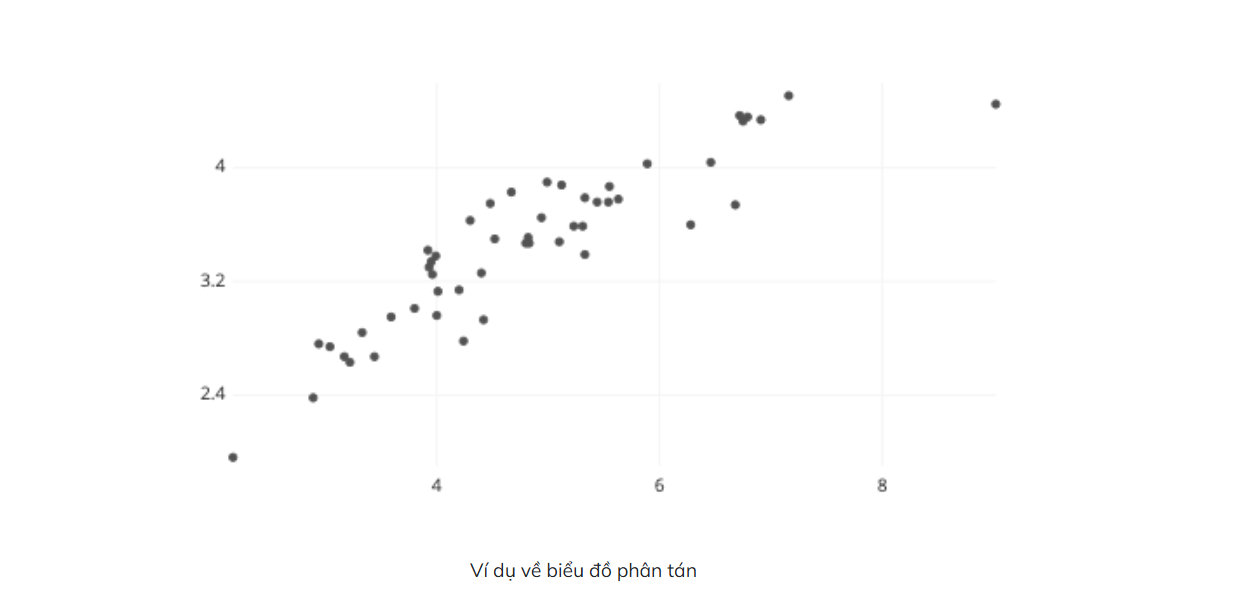
2. Quan sát gì từ scatterplot?
Tương quan dương: Cả hai biến cùng tăng
Tương quan âm: Một biến tăng, một biến giảm
Không tương quan: Không có mẫu hình rõ ràng
Đường hồi quy tuyến tính (Line of Best Fit)
1. Định nghĩa
Là đường thẳng tốt nhất mô tả xu hướng tổng quát của các điểm trên biểu đồ phân tán. Đường này giúp dễ dàng phát hiện quy luật giữa hai biến.
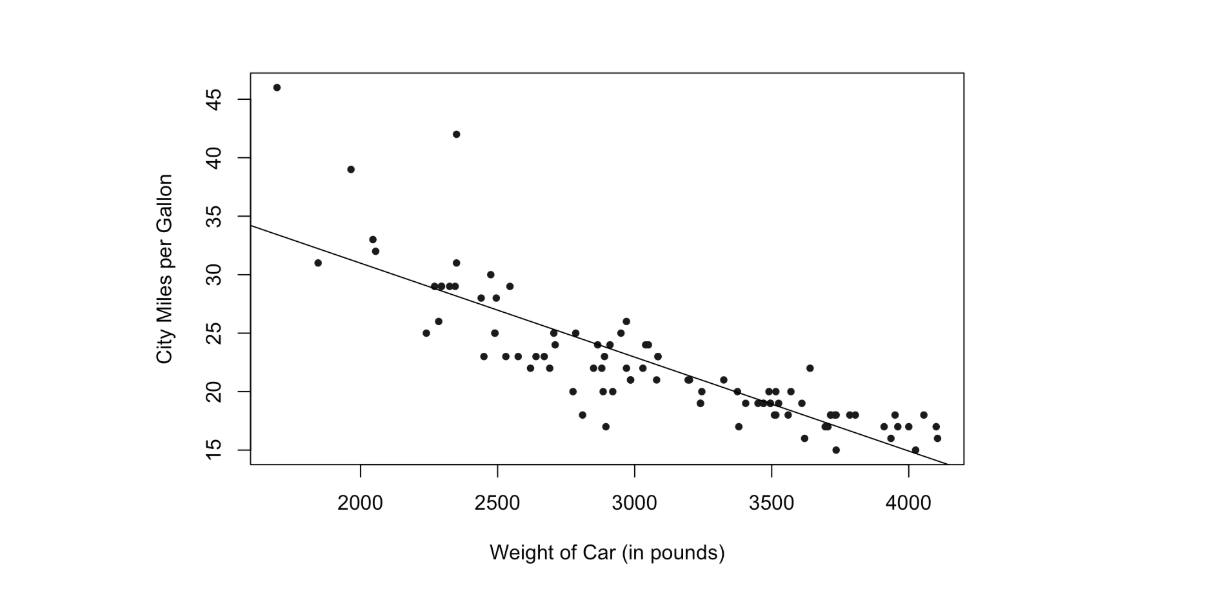
2. Ý nghĩa
– Hệ số góc (slope): Mức thay đổi của biến phụ thuộc theo biến độc lập
– Giao điểm trục y (y-intercept): Giá trị khởi đầu khi biến độc lập bằng 0
❗ Gợi ý xu hướng nhưng không thể hiện quan hệ nhân quả
Mẹo & thủ thuật
Dùng phương trình đường thẳng để dự đoán:
Ví dụ: y = 2x + 50 ⟹ x = 5 ⟹ y = 60
? Slope càng lớn thì biến phụ thuộc thay đổi càng mạnh
? Y-intercept cho biết giá trị gốc (baseline)
Ví dụ 1: Tìm phương trình đường hồi quy
Dữ liệu: (2, 3), (4, 5), (6, 7), (8, 9)
Tính slope:
(5−3)/(4−2) = 1Dùng (2, 3) để tìm y-intercept:
3 = 1×2 + b ⟹ b = 1✅ Phương trình:
y = x + 1
Ví dụ 2: Giải thích y = 2x + 50
Slope = 2: Mỗi giờ học tăng thì điểm tăng 2 điểm
Y-intercept = 50: Không học gì vẫn được 50 điểm
Dự đoán từ dữ liệu (Predictions)
Dựa vào đường hồi quy, bạn có thể:
– Nội suy (interpolation): Dự đoán trong khoảng dữ liệu
– Ngoại suy (extrapolation): Dự đoán ngoài khoảng dữ liệu
Ví dụ: y = 2x + 50 ⟹ x = 5 ⟹ y = 60
⚠ Ngoại suy có thể không chính xác vì vượt quá phạm vi quan sát.
Mẹo khi dự đoán
✅ Dùng đường hồi quy, không dựa vào điểm lẻ
✅Tránh dự đoán quá xa dữ liệu gốc
✅Nhận diện nội suy vs ngoại suy để đánh giá độ tin cậy
Ví dụ 1: Dự đoán với y = 3x + 40
x = 7 ⟹ y = 3×7 + 40 = 61
✅ Dự đoán điểm là 61
Ví dụ 2: Dự đoán với x = 20?
Quá xa dữ liệu ban đầu ➡ Không đáng tin cậy (ngoại suy)
Khớp hàm (Fitting Functions)
Trong SAT, bạn có thể phải chọn hàm phù hợp với biểu đồ phân tán. Các dạng thường gặp:
✅ Hàm tuyến tính (linear): y = mx + b
✅ Hàm bậc hai (quadratic): y = ax² + bx + c
Ví dụ: Tìm hàm tuyến tính phù hợp
Điểm dữ liệu gần đúng: (2, 6), (4, 12)
Tính slope:
(12−6)/(4−2) = 3Dùng (2, 6) tìm y-intercept:
6 = 3×2 + b ⟹ b = 0
✅ Hàm phù hợp:y = 3x
✨ Mẹo chọn hàm phù hợp
– Vẽ sơ đồ xu hướng (đường thẳng hoặc parabol)
– So khớp slope và intercept với lựa chọn đề cho
– Với hàm bậc hai, để ý hướng cong và đỉnh (vertex)
✅ Tổng kết:
Dựa vào những kiến thức trên bạn có thể tham khảo đề thi thử SAT miễn phí mục tiêu 1500+ tại đây
| Kỹ năng | Bạn cần nắm vững |
|---|---|
| Đọc scatterplot | Phát hiện xu hướng, loại tương quan |
| Đường hồi quy | Tìm phương trình, diễn giải slope & intercept |
| Dự đoán | Phân biệt nội suy vs ngoại suy, áp dụng đúng cách |
| Khớp hàm | Nhận dạng tuyến tính hay bậc hai dựa vào xu hướng dữ liệu |
Thông tin liên quan
Bí quyết xử lý câu hỏi nhận định thống kê trong SAT
Câu hỏi về nhận định thống kê trong SAT thường đánh đố thí sinh bằng những biểu đồ, dữ kiện và lập luận phức tạp. Bài viết này sẽ hướng dẫn bạn cách nhận diện bẫy, phân tích logic và lựa chọn đáp án chính xác một cách hiệu quả nhất.
Nắm vững bất phương trình một ẩn và hai ẩn để làm tốt phần Toán SAT
Khám phá cách giải nhanh và chính xác các câu hỏi về bất đẳng thức tuyến tính một và hai ẩn trong bài thi SAT. Hướng dẫn từng bước, mẹo tránh sai lầm phổ biến và cách xử lý trường hợp cần đổi chiều bất đẳng thức. Thích hợp cho học sinh ôn luyện toán và chuẩn bị cho kỳ thi chuẩn hóa quốc tế.
Làm chủ kiến thức diện tích và thể tích để đạt điểm cao phần Toán SAT
Khám phá hướng dẫn toàn diện giúp bạn làm chủ các bài toán về diện tích và thể tích – một chủ điểm quan trọng trong phần toán SAT. Bài viết cung cấp chiến lược từng bước, công thức thiết yếu, ví dụ minh họa và bài tập thực hành nhằm củng cố kỹ năng hình học và cải thiện điểm số hiệu quả.
Tự tin xử lý mọi câu hỏi về đường tròn trong SAT
Khám phá cách giải các câu hỏi về hình tròn trong kỳ thi SAT một cách dễ hiểu và hiệu quả. Học công thức chu vi, diện tích, cung tròn và hình quạt qua ví dụ thực tế và mẹo làm bài nhanh.
Bí quyết xử lý phân bố và đại lượng đo lường trong SAT
Các câu hỏi về phân bố dữ liệu và các đại lượng đo lường như trung bình, trung vị, độ lệch chuẩn… thường xuyên xuất hiện trong phần toán SAT. Bài viết này sẽ giúp bạn hiểu rõ ý nghĩa các khái niệm, cách phân tích đồ thị và áp dụng chiến lược giải nhanh – chính xác.
Làm chủ các câu hỏi về đường thẳng, góc và tam giác trong kỳ thi SAT
Nắm vững các kiến thức về đường thẳng, góc và tam giác là chìa khóa để giải quyết hiệu quả các câu hỏi hình học trong SAT. Bài viết cung cấp hướng dẫn toàn diện kèm mẹo, ví dụ minh họa và bài tập thực hành giúp bạn tránh lỗi sai phổ biến và tăng tốc độ làm bài.
