Câu hỏi về phương trình tuyến tính hai biến trong kỳ thi SAT

Việc hiểu rõ phương trình bậc nhất hai ẩn là chìa khóa để bạn thành thạo phần toán trong kỳ thi SAT. Bài viết này sẽ phân tích các kỹ thuật giải dạng bài này kèm theo ví dụ minh họa rõ ràng cho từng phương pháp.

📚 Giới thiệu về phương trình bậc nhất hai ẩn

Phương trình bậc nhất hai ẩn là một phần quen thuộc trong phần toán SAT. Dạng bài này không chỉ kiểm tra kỹ năng đại số mà còn khả năng diễn giải các tình huống thực tế thành biểu thức toán học.

✔️ Trọng tâm của dạng toán này là hiểu phương trình dưới dạng đồ thị đường thẳng, mối quan hệ giữa các hệ số và hằng số.

🧾 Cấu trúc phương trình

🧩 Các phương trình tuyến tính trong hai biến thường được trình bày ở dạng chuẩn: ax + by = c
Trong đó:

a, b, c là các hằng số

x, y là hai biến

👉 Dạng này giúp nhận biết nhanh cấu trúc và thành phần phương trình. Các hệ số a, b sẽ ảnh hưởng đến độ nghiêng (hệ số góc) và giao điểm trục y.

📈 Dạng y = mx + b (dạng hàm số bậc nhất)

Ở dạng này:

m: hệ số góc (độ dốc đường thẳng)

b: tung độ giao điểm với trục y

Ví dụ: y = 2x + 3
✅ Độ dốc = 2
✅ Cắt trục y tại (0, 3)

🔍 Khi thay đổi a, b, c trong ax + by = c, đường thẳng sẽ thay đổi độ dốc hoặc tịnh tiến lên/xuống, ví dụ:

2x + 3y = 6 → tăng a thành 4 → 4x + 3y = 6 👉 dốc lớn hơn

🔧 Biến đổi phương trình

Bạn cần biết cách chuyển đổi giữa các dạng:

➡️ Chuyển từ dạng chuẩn sang dạng y = mx + b:

Ví dụ: 2x + 3y = 6

Trừ 2x hai vế: 3y = -2x + 6

Chia cả hai vế cho 3: y = -2/3x + 2

📝 Dạng bài toán thực tế (word problems)

SAT thường đưa ra các bài toán dạng:

Ví dụ: 3x + 5y = 11
Trong đó:

x: số quả táo

y: số quả cam
👉 Táo giá 3, cam giá 5

Hiểu dạng phương trình sẽ giúp bạn diễn giải ý nghĩa thực tế, tìm giá từng món, hoặc số lượng phù hợp.

📊 Biểu diễn bằng đồ thị

Hiểu đồ thị giúp bạn hình dung mối quan hệ giữa x và y:

🟢 Ví dụ: y = 2x + 3

Độ dốc = 2 → đường tăng

Cắt trục y tại (0, 3)

🔴 Ví dụ: y = -x - 2

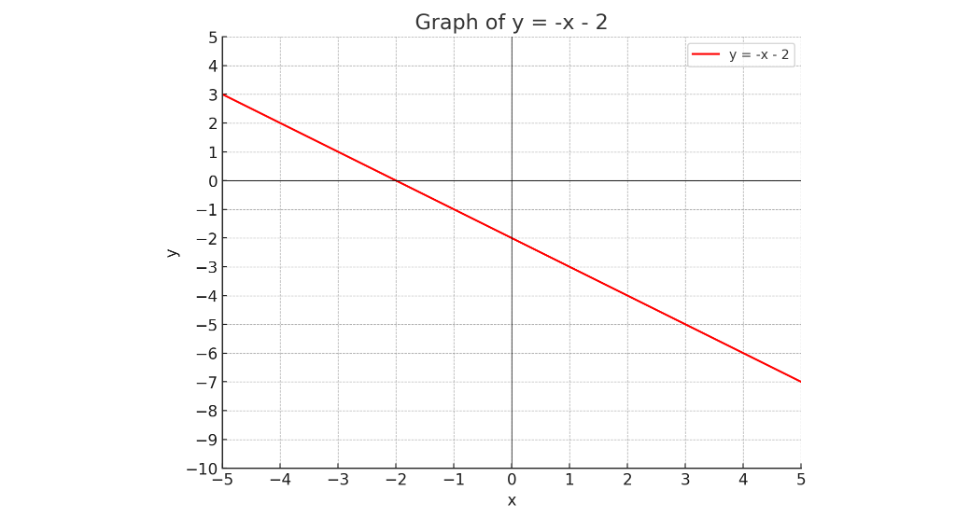
Độ dốc âm → đường giảm

Cắt trục y tại (0, -2)

📌 Đồ thị cho bạn thông tin trực quan về:

Giao điểm hai đường

Độ dốc

Tương quan giữa biến trong bài toán thực tế

🧮 Cách giải hệ phương trình hai ẩn

Câu hỏi tuyến tính phổ biến nhất trong SAT là giải phương trình. Giải phương trình tuyến tính trong hai biến thường liên quan đến việc tìm giá trị của x, y thỏa mãn đồng thời 2 phương trình. Điều này có thể được thực hiện bằng nhiều phương pháp khác nhau, chẳng hạn như biểu đồ (đã thảo luận ở trên), thay thế hoặc loại bỏ.

1️⃣ Phép thế (Substitution)

Ví dụ: y = 2x + 3 và y = -x - 2

Do cùng bằng y, ta đặt 2x + 3 = -x - 2

Giải ra x, sau đó thay vào tìm y

2️⃣ Phép khử (Elimination)

Ví dụ: 2x + 3y = 6 và x - y = 2

Nhân phương trình thứ 2 với 3 → 3x - 3y = 6

Cộng với phương trình đầu → khử y → tìm x, sau đó tìm y

⚠️ Trường hợp đặc biệt:

❌ Không có nghiệm

Ví dụ: nếu giải ra 0 = 5 → vô lý → hệ phương trình vô nghiệm

♾️ Vô số nghiệm

Nếu giải ra 0 = 0 đúng với mọi giá trị → vô số nghiệm
→ Cả hai đều là đáp án hợp lệ trong SAT

=> Xem ngay: Đề Thi SAT 1 - Thi thử SAT Online - Đề Nâng Cao, Cấp Độ Khó Tối Đa

✅ Kiểm tra lời giải

Thay thế các giải pháp trở lại vào phương trình

Luôn thay nghiệm vào phương trình gốc để kiểm tra:

Ví dụ:
Giải ra x = 1, y = 3 cho hệ:

2x + 3y = 6

x − y = 2

→ Thay vào:

2(1) + 3(3) = 11 ❌

1 − 3 = -2 ✅

⇒ Có sai, cần kiểm tra lại

📉 Kiểm tra bằng đồ thị

Một phương pháp kiểm tra khác bao gồm vẽ đồ thị cả hai phương trình và quan sát xem giải pháp có tương ứng với điểm giao nhau hay không. Đối với các phương trình tuyến tính, kiểm tra đồ họa này có thể khá hiệu quả, đặc biệt là đối với người học trực quan.

Trong ví dụ trên, việc biểu diễn đồ thị của cả hai phương trình sẽ cho thấy liệu điểm (1, 3) có nằm tại giao điểm của cả hai đường thẳng hay không.

🔍 Ví dụ minh họa

✏️ Ví dụ 1: Phép thế

Phương trình:
y = 2x + 1 và y = x - 2

Giải:
2x + 1 = x - 2 → x = -3
Thay vào: y = -5
✅ Nghiệm: x = -3, y = -5

✏️ Ví dụ 2: Phép khử

Phương trình:
3x + 2y = 6 và 6x − 2y = 12

Cộng hai phương trình:
9x = 18 → x = 2
Thay vào: 3(2) + 2y = 6 → 2y = 0 → y = 0
✅ Nghiệm: x = 2, y = 0

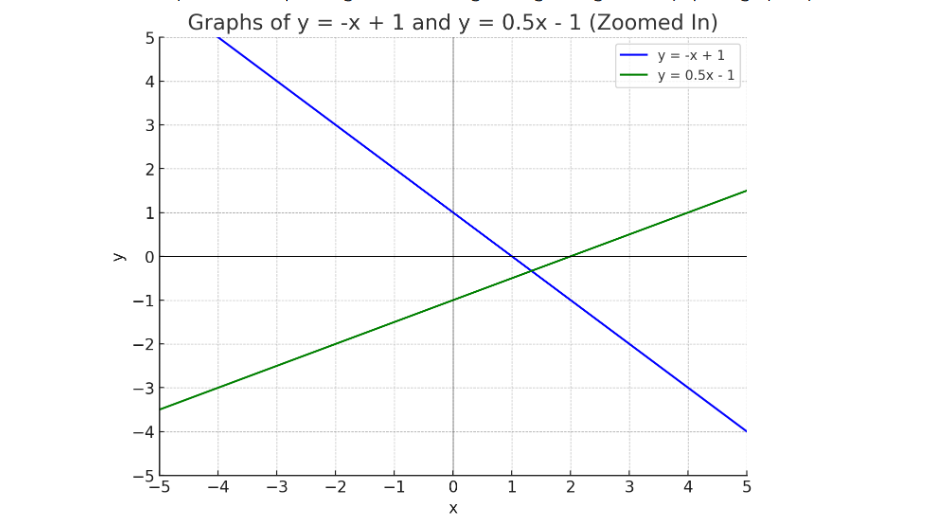
✏️ Ví dụ 3: Đồ thị

Phương trình:
y = −x + 1 và y = (1/2)x − 1
Vẽ đồ thị → Giao điểm tại: x = 4/3, y = −1/3

✅ Nghiệm gần đúng: (4/3, −1/3)