Nắm chắc kiến thức lượng giác để chinh phục phần Toán SAT

Giới thiệu

Lượng giác thường được gọi là trig, xử lý mối quan hệ giữa các góc và cạnh của tam giác. Nó liên quan đến việc sử dụng tam giác vuông để tìm số đo góc và độ dài cạnh còn thiếu. Trong hướng dẫn này, chúng tôi sẽ đề cập đến các tính chất đặc biệt của tam giác vuông, cách chúng liên quan đến đường tròn đơn vị và các hàm lượng giác cốt lõi (sin, cos và tan).

?Nhìn chung, lượng giác là một chủ đề khá nâng cao và khó hiểu, và mặc dù những câu hỏi này chắc chắn xuất hiện thường xuyên trong bài thi SAT nhưng thường chỉ có một hoặc hai câu hỏi trong mỗi kỳ thi.

Vì vậy, nếu bạn chỉ có vài tuần để học và chưa quen với lượng giác, chúng tôi khuyên bạn nên củng cố hiểu biết của mình về các chủ đề rộng hơn như đại số và hàm phi tuyến tính trước vì những câu hỏi này xuất hiện thường xuyên hơn nhiều.

Tuy nhiên, nếu bạn có thời gian, lượng giác chắc chắn đáng để tìm hiểu vì đây là điều kiện tiên quyết cần thiết cho phép tính vi phân và các khóa học toán ở trình độ đại học.

SOHCAHTOA & Định lý Pythagoras

SOHCAHTOA là một mẹo ghi nhớ nổi tiếng để ghi nhớ mối quan hệ giữa các góc và các cạnh của một tam giác vuông.

Sine (sin) = Đối / Huyền

Cosine (cos) = Kề / Huyền

Tangent (tan) = Đối / Kề

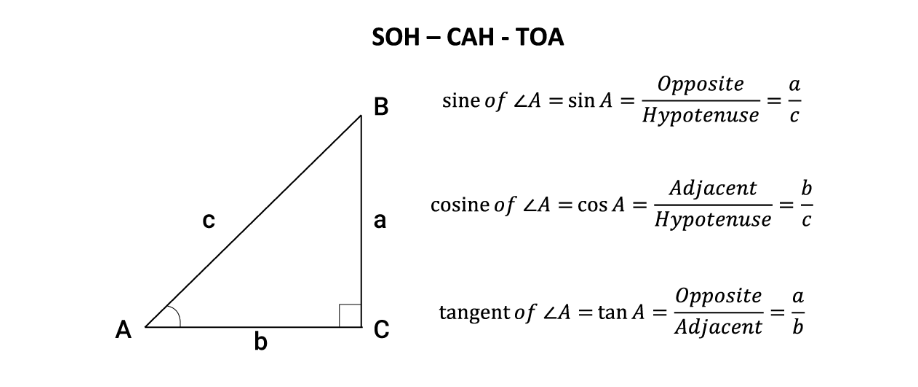
Dùng để tìm độ dài cạnh hoặc góc còn thiếu trong tam giác vuông.

Định lý Pythagoras:  a²+b²=c²

Áp dụng cho tam giác vuông, giúp tìm cạnh còn thiếu hoặc xác định tam giác có vuông hay không.

Ví dụ:

Tìm sin, cos, tan của góc 30° trong tam giác có cạnh huyền dài 2:

sin(30°) = 1/2

cos(30°) = √3/2

tan(30°) = 1/√3

Hàm lượng giác nghịch đảo

Ngoài sin, cos và tan, còn có ba hàm lượng giác nghịch đảo: secant (sec), cosecant (csc) và cotangent (cot).

Các hàm này là các nghịch đảo của cos, sin và tan. Hiểu các hàm nghịch đảo này có thể cung cấp thêm các công cụ để giải các bài toán lượng giác.

sec(x) = 1 / cos(x)

csc(x) = 1 / sin(x)

cot(x) = 1 / tan(x)

 

Các hàm nghịch đảo này hữu ích trong nhiều bài toán lượng giác, đặc biệt là khi xử lý các tỷ số của các cạnh không được cung cấp trực tiếp. ? Ví dụ, nếu bạn biết sin của một góc, bạn có thể dễ dàng tìm cosecant bằng cách lấy nghịch đảo. Điều này có thể đơn giản hóa các phép tính và cung cấp các cách thay thế để giải quyết các bài toán.

Điều quan trọng là phải nhớ mối quan hệ giữa các hàm này và các hàm nghịch đảo của chúng. Ví dụ, secant tương ứng với cosine, cosecant tương ứng với sin và cotangent tương ứng với tangent. Ghi nhớ các mối quan hệ này sẽ giúp bạn giải quyết các bài toán lượng giác hiệu quả hơn - rất dễ mất thời gian quý báu trong kỳ thi vì tìm kiếm công thức!

? Ví dụ:

Nếu sin(45°) = √2/2 thì
⇒ csc(45°) = 1 / (√2/2) = √2

Các đẳng thức lượng giác

Đẳng thức Pythagoras:

sin²x + cos²x = 1

1 + tan²x = sec²x

1 + cot²x = csc²x

Đẳng thức thương:

tan(x) = sin(x)/cos(x)

cot(x) = cos(x)/sin(x)

Các hằng số này hữu ích cho việc rút gọn biểu thức và giải phương trình lượng giác nhanh chóng.

Ví dụ:

Tính sin(45°) × sec(45°)
Ta có: sin(45°) = √2/2  and sec⁡(45°) = 1/cos⁡(45°) =1/ √2/2 = √2​.

=> sin(45°) × sec(45°) = √2/2 × √2 = 2/2 = 1

Đơn vị Radian

Radian đo góc dựa trên bán kính của hình tròn. Một vòng quay hoàn chỉnh quanh một hình tròn là2P2 trangradian, tương đương với 360 độ. Radian cung cấp một cách đo góc thay thế thường thuận tiện hơn trong toán học nâng cao và phép tính.

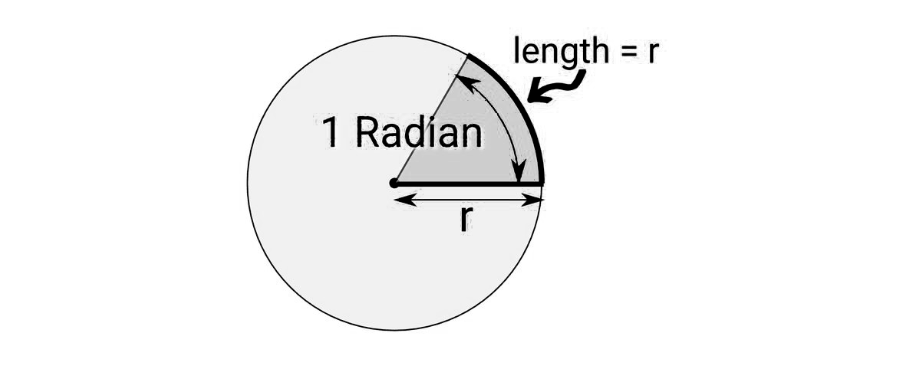
Chuyển đổi:

Degrees → Radians: ° × π/180

Radians → Degrees: rad × 180/π

Ví dụ:

Chuyển đổi 45 độ sang radian.

Giải pháp: 45° = 45 × π/180 = π/4 radian

Vòng tròn đơn vị

Đường tròn đơn vị là đường tròn có bán kính 1, tâm tại gốc tọa độ. Nó cho phép chúng ta mở rộng các hàm lượng giác ra ngoài tam giác vuông, cung cấp các giá trị cho bất kỳ góc nào. Phương trình của đường tròn đơn vị là x²+y²=1.

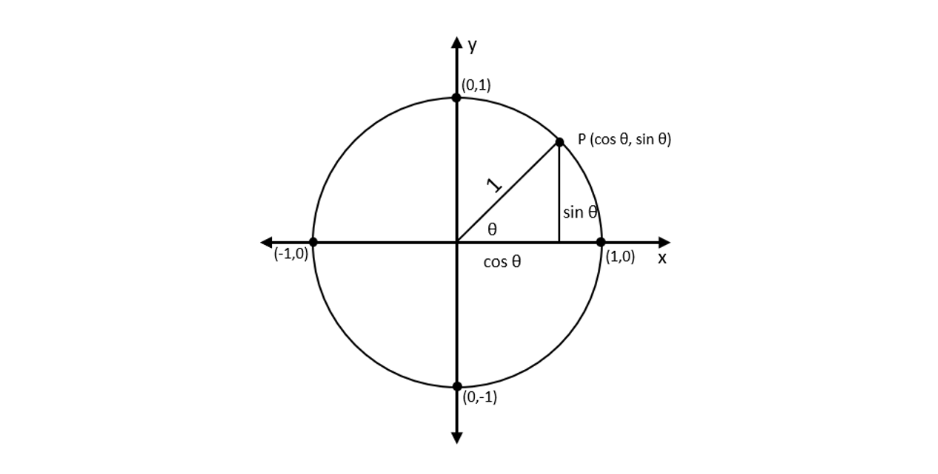
Đường tròn đơn vị cung cấp một cách để tìm giá trị của các hàm lượng giác cho các góc lớn hơn 90 độ và cho các góc âm. Bằng cách mở rộng các khái niệm tam giác vuông sang đường tròn đơn vị, chúng ta có thể xác định sin, cosin và tan của bất kỳ góc nào.

Để sử dụng đường tròn đơn vị, chúng ta tìm tọa độ của điểm mà cạnh cuối của góc giao với đường tròn. Tọa độ x tương ứng với cosin của góc và tọa độ y tương ứng với sin của góc. Phương pháp này áp dụng cho mọi góc, bao gồm cả những góc ở các góc phần tư khác nhau.

Đường tròn đơn vị cũng giới thiệu khái niệm góc tham chiếu, được sử dụng để tìm giá trị lượng giác cho các góc nằm ngoài góc phần tư thứ nhất.

Góc tham chiếu là góc nhọn được tạo thành giữa cạnh cuối của góc đã cho và trục x. Bằng cách sử dụng góc tham chiếu và đường tròn đơn vị, chúng ta có thể tìm giá trị của các hàm lượng giác cho bất kỳ góc nào.

Các công thức hữu ích cho phần này:

sin(θ) = y

cos(θ) = x

tan(θ) = y / x

Dùng để tìm giá trị sin, cos, tan với mọi góc (kể cả góc âm & >90°)

Ví dụ:

Tìm tọa độ của điểm trên đường tròn đơn vị tương ứng với một góc π/3 

Giải pháp: Tọa độ điểm trên vòng tròn: (cos(π/3), sin(π/3)) = (1/2, √3/2)

Đồ thị hàm lượng giác

Hiểu cách vẽ đồ thị hàm sin, cos và tan là rất quan trọng. Đồ thị của các hàm này là tuần hoàn, lặp lại sau mỗi 2π đối với sin và cos, và sau mỗi π đối với tan. Các dạng chuẩn là y=sin(x), y=cos⁡(x), và y=tan(x).

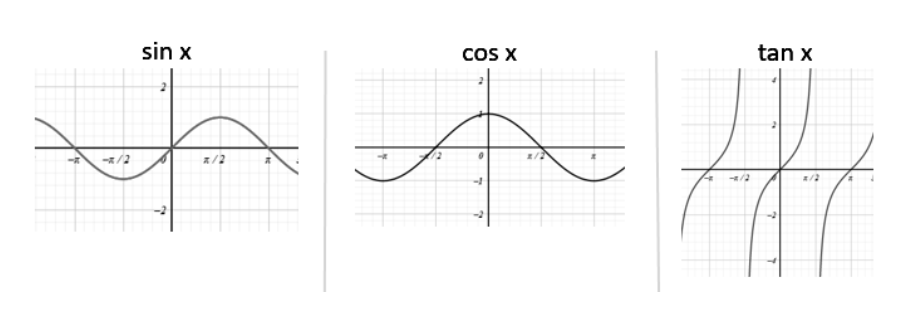
Biến đổi đồ thị:

Hàm tổng quát: y=Asin(Bx+C)+D

A: biên độ

B: ảnh hưởng đến chu kỳ (chu kỳ = 2π/B)

C: dịch ngang

D: dịch dọc

Ví dụ:

Tìm chu kỳ của y = sin(3x) → Chu kỳ = 2π / 3

Các tam giác vuông đặc biệt

1. Tam giác 30°–60°–90°

Tam giác 30-60-90 là tam giác vuông đặc biệt có các góc là 30°, 60° và 90°. Độ dài các cạnh theo tỷ lệ 1 : √3 : 2. Điều này có nghĩa là nếu cạnh ngắn hơn (đối diện với góc 30°) có độ dài là a, thì cạnh dài hơn (đối diện với góc 60°) sẽ có độ dài là a√3 và cạnh huyền sẽ có độ dài là 2a.

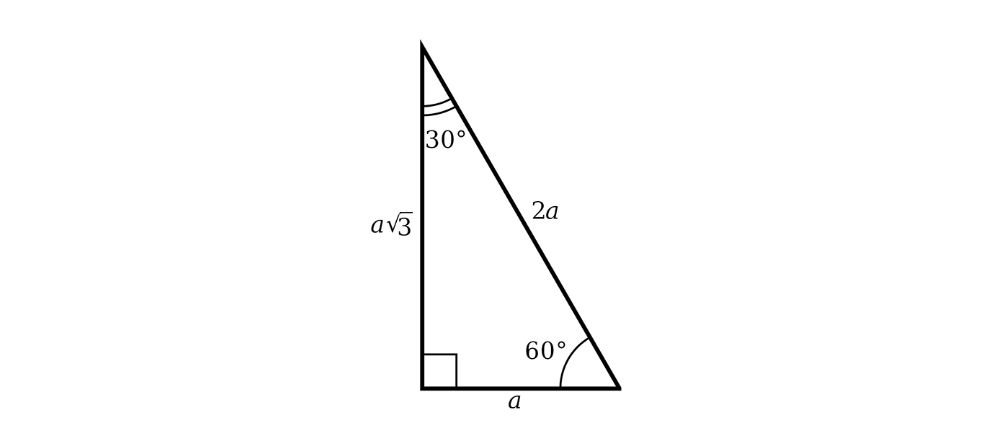
2. Tam giác 45°–45°–90°

Tam giác 45-45-90 là một tam giác vuông đặc biệt khác có các góc là 45°, 45° và 90°. Chiều dài các cạnh theo tỷ lệ 1 : 1 : √2. Điều này có nghĩa là nếu một cạnh có chiều dài là a, thì cạnh còn lại cũng sẽ có chiều dài là a, và cạnh huyền sẽ có chiều dài là a√2.

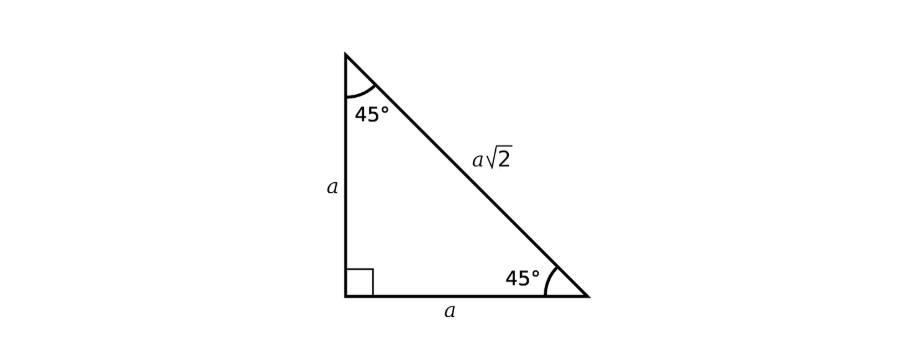
✅ Ghi nhớ các tỉ lệ này giúp giải nhanh mà không cần công thức hoặc định lý.

Kết luận

Lượng giác là phần nâng cao nhưng nếu bạn hiểu rõ các công thức, tỉ lệ và cách sử dụng vòng tròn đơn vị, bạn sẽ dễ dàng làm chủ các câu hỏi SAT và sẵn sàng cho Toán cấp cao hơn.
=> Cập nhật: Các mẫu đề thi thử SAT online mới nhất 2025.